REAL LIFE APPLICATION OF FOURIER SERIES

let's first deal Fourier series with modelling nature. what it actually signifies in real world?

It was the research in ancient times. in that time, scientists used to make assumption that moon revolves around Earth in circular path not elliptical which was corrected later by Kepler. it was the assumption that moon revolves around Earth in circular path at a distance r with velocity v.

We can represent moon as a particle in circular path. that is, let p(X,Y) be a point which is at distance r from origin (Centre of earth) and angle theta from x-axis. Also, p is at distance y from x-axis and x from y-axis. like this,

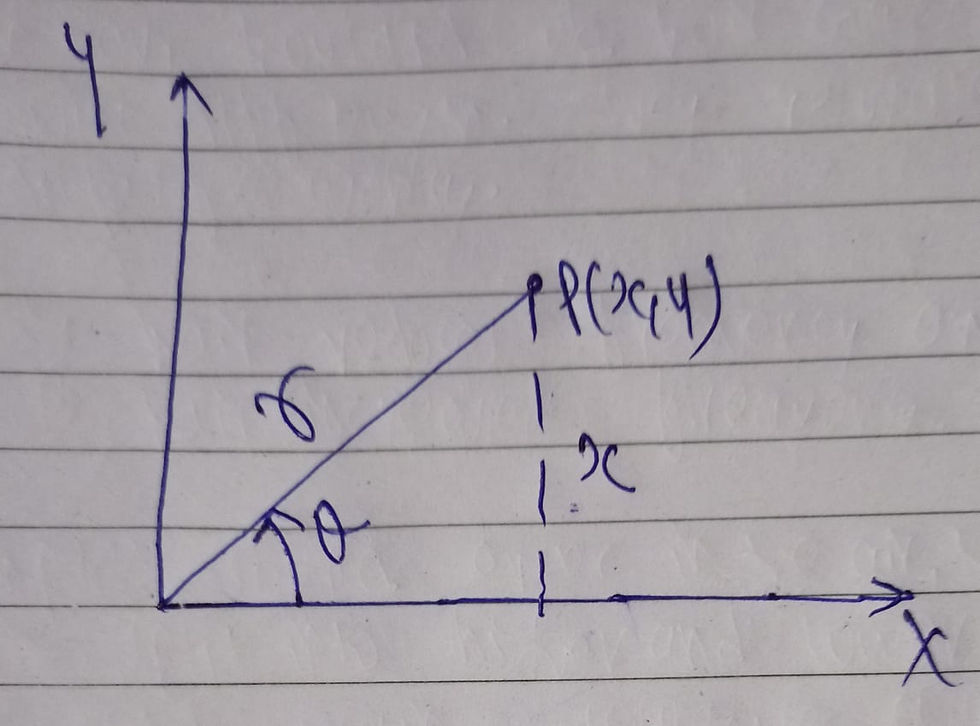
Now, we can represent the position of moon in cartesian or polar form. that is,

z=x+iy or z=re^i(theta). also, theta=(angular frequency)*(time). therefore,

z=re^iwt. this is the position of moon varying with time. also, this equation represent circle with constant radius a(assumption). e^iwt represent particle moving in circle.

we all know moon changes its position with time along different path. like this,

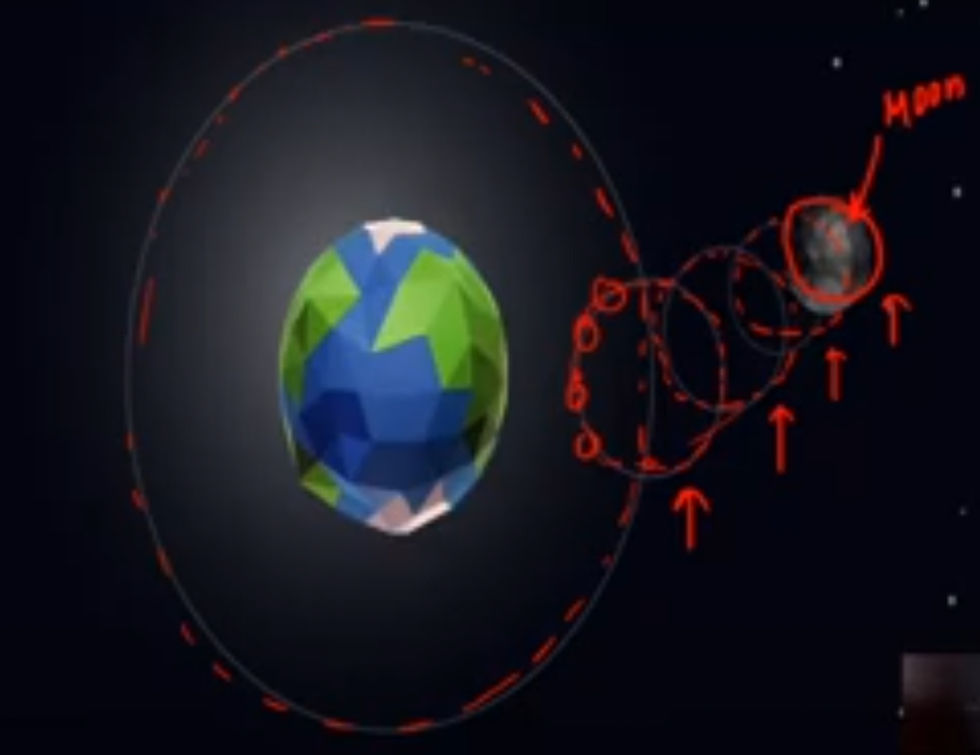
All different path have different radii and we can represent different radii in vector form. like this,

This is the reason why we get moon sometimes bright, large or small because of changing frequency and position. Therefore,

we can represent the series as z=R1e^iw1t+R2e^iw2t+R3e^iw3t.....

that is, z=summation(-infinity to infinity)[Rk.e^iw0t] where Rk=R1,R2,R3... and wo=w1,w2,w3....

This series is somewhat called Fourier series. also, this is how orbit works.

That is why moon orbital motion is periodically varying along those path with a period of 28 month and is modelled using Fourier series.

We got these conclusions from this series-

1. motion of earth around path is periodic.

2. Also, circular path consists both sine and cosine function or, circle can be represented by sine and cosine.

3. combination of sine and cosine gives superposition of wave.

In mathematical form, we can define Fourier series as:

A Fourier series is an expansion of a function in a series of sines and cosines such as

f(x)=a0/2 +summation(n=1 to infinity)[ancos(n*pi*x/L)+bnsin(n*pi*x/L)]

where n=1,2,3.... and L= half of period of function f(x).

Fourier series make use of the orthogonality relationships of the sine and cosine functions. it allows us to model any arbitrary periodic signal with a combination of sines and cosines.

Fourier series is everywhere. Now we'll look into its application.

Application of Fourier series:

1. inner ear: in ear, thousands of hair cells are present with different length. They resonates with different frequencies. long hair reduces frequency and short hair increases frequency. so when complex sound enter in the air, the hair cell split into higher and lower frequency and brain recognize a simple bunch of wave and frequency. like this,

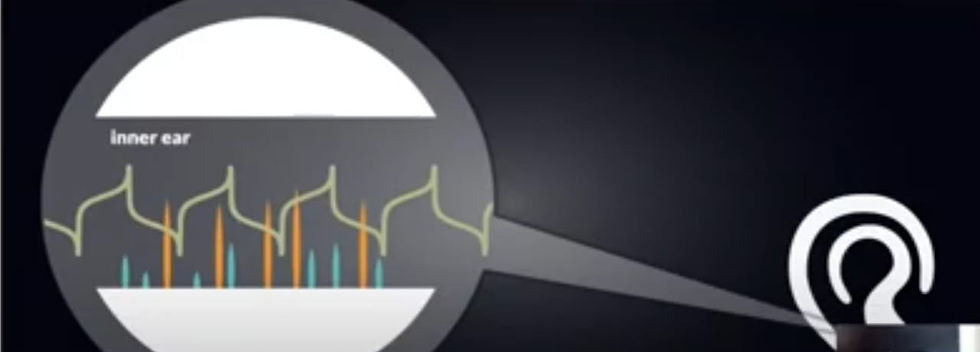
so we had seen combination of sine and cosine waves and how they increase or decrease frequency. This is superposition of sine and cosine waves in given figure.

Every superimposed wave is Fourier series.

2. wave theory: in wave theory, we learnt superimpose of two waves which create disturbance on a screen. like this,

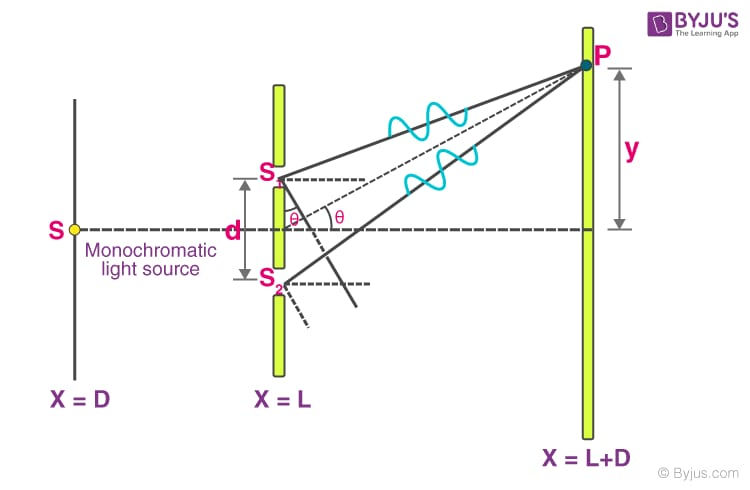
This disturbance has intensity which is known as superposition of waves.

that is, I=I1 +I2 + 2*sqrt(I1*I2)cos(theta). Here, Imax gives constructive interference where we see bright band and Imin gives destructive interference where we see dark band.

Also, intensity is directly proportional to (amplitude)^2 which means maximum amplitude gives bright band and min amplitude gives dark band.

3.Finding solutions of heat equation. These solutions have had lot of applications in engineering. that is, partial derivative of (fi with respect to t)=D*double partial derivative of (fi with respect to x) where D is coefficient of conductivity.

4.without Fourier, we could only encode data like old FM radios, and we'd have to wait 1 minute to load this page or leave the laptop all night downloading a single youtube video.

5.If Fourier wasn't used, phone calls would sound like pre-ww2 radios or even worse. people would have to talk louder the farther away they called from, calls would be interrupted by noise every time people walked behind a tree or around cars because of reflections.

HOPE YOU GUYZ UNDERSTOOD THE IMPORTANCE OF FOURIER SERIES.

DON'T FORGET TO COMMENT THE FEEDBACK AND YOUR OPINION.

THANK YOU.